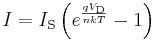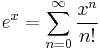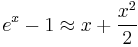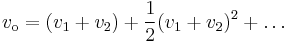Frequency mixer
In electronics a mixer or frequency mixer is a nonlinear electrical circuit that creates new frequencies from two signals applied to it. In its most common application, two signals at frequencies f1 and f2 are applied to a mixer, and it produces new signals at the sum f1 + f2 and difference f1 - f2 of the original frequencies. Other frequency components may also be produced in a practical frequency mixer.
Mixers are widely used to shift signals from one frequency range to another, a process known as heterodyning, for convenience in transmission or further signal processing. For example, a key component of a superheterodyne receiver is a mixer used to move received signals to a common intermediate frequency. Frequency mixers are also used to modulate a carrier frequency in radio transmitters.
Contents[hide] |
Types
Passive mixers use one or more diodes and rely on the non-linear relation between voltage and current to provide the multiplying element. In a passive mixer, the desired output signal is always of lower power than the input signals. Active mixers can increase the strength of the product signal. Active mixers improve isolation between the ports, but may have higher noise and more power consumption; an active mixer can be less tolerant of overload.
Mixers may be built of discrete components, may be part of integrated circuits, or can be delivered as hybrid modules.
Mixers may also be classified by their topology. Unbalanced mixers allow some of the input signal power to pass through to the output. A single-balanced mixer is arranged so that the local oscillator, (or RF) signal port, cancels and cannot pass through to the output. A doubly balanced mixer has symmetrical paths for both inputs, and will have no output if either input signal is not present.
Selection of a mixer type is a trade off for a particular application. Mixer circuits are characterized by conversion gain, and noise figure.[1] Balanced and double-balanced designs allow less of the input signals to feed through to the output.
Nonlinear electronic components that are used as mixers include diodes, transistors biased near cutoff, and at lower frequencies, analog multipliers. Ferromagnetic-core inductors driven into saturation have also been used. In nonlinear optics, crystals with nonlinear characteristics are used to mix two frequencies of laser light to create optical heterodynes.
Diode
A diode can be used to create a simple unbalanced mixer. This type of mixer produces the original frequencies as well as their sum and their difference. The importance of the diode is that it is non-linear (or non-Ohmic), which means its response (current) is not proportional to its input (voltage). The diode therefore does not reproduce the frequencies of its driving voltage in the current through it, which allows the desired frequency manipulation. Certain other non-linear devices such as tunnel diodes or Gunn diodes can be utilized similarly.
The current I through an ideal diode as a function of the voltage V across it is given by
where what is important is that V appears in e's exponent. The exponential can be expanded as
and can be approximated for small x (that is, small voltages) by the first few terms of that series:
Suppose that the sum of the two input signals 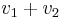 is applied to a diode, and that an output voltage is generated that is proportional to the current through the diode (perhaps by providing the voltage that is present across a resistor in series with the diode). Then, disregarding the constants in the diode equation, the output voltage will have the form
is applied to a diode, and that an output voltage is generated that is proportional to the current through the diode (perhaps by providing the voltage that is present across a resistor in series with the diode). Then, disregarding the constants in the diode equation, the output voltage will have the form
The first term on the right is the original two signals, as expected, followed by the square of the sum, which can be rewritten as 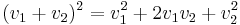 , where the multiplied signal is obvious. The ellipsis represents all the higher powers of the sum which we assume to be negligible for small signals.
, where the multiplied signal is obvious. The ellipsis represents all the higher powers of the sum which we assume to be negligible for small signals.
Switching
Another form of mixer operates by switching, with the smaller input signal being passed inverted or uninverted according to the phase of the local oscillator (LO). This would be typical of the normal operating mode of a packaged double balanced mixer module such as an SBL-1, with the local oscillator drive considerably higher than the signal amplitude.
The aim of a switching mixer is to achieve linear operation over the signal level, and hard switching driven by the local oscillator. Mathematically the switching mixer is not much different from a multiplying mixer, just because instead of the LO sine wave term we would use the signum function. In the frequency domain the switching mixer operation leads to the usual sum and difference frequencies, but also to further terms e.g. +-3*fLO, +-5*fLO, etc. The advantage of a switching mixer is that it can achieve - with the same effort - a lower noise figure (NF) and larger conversion gain. This come because the switching diodes or transistors act either like a low resistor (switch closed) or large resistor (switch open) and in both cases only minimum noise is added. From the circuit perspective many multiplying mixers can be used as switching mixers, just by increasing the LO amplitude. So RF engineers simply talk about mixers, and mean switching mixers.
Applications
The mixer circuit can be used not only to shift the frequency of an input signal as in a receiver, but also as a product detector, modulator, phase detector or frequency multiplier.[2] For example a communications receiver might contain two mixer stages for conversion of the input signal to an intermediate frequency, and another mixer employed as a detector for demodulation of the signal.
See also
- Frequency multiplier
- Optical heterodyne detection
- Gilbert cell
- Intermodulation
- Pentagrid converter
- Product detector
- Ring modulation
- Rusty bolt effect
- Subharmonic mixer
- Third-order intercept point
References
- ^ D.S. Evans, G. R. Jessop, VHF-UHF Manual Third Edition, [[Radio Society of Great Britain, 1976, page 4-12
- ^ Paul Horowitz, Winfred Hill The Art of Electronics Second Edition, Cambridge University Press 1989, pp. 885-887
External links
This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".
|
||||||||||||||||||||||||||||||||